(条件:周囲-自由端 N=500)

Option Explicit
Const N = 100 '分割数
Const ccc = 1
Const dd = 1
Sub 波動方程式10()
Dim t As Double
Dim dt As Double
Dim i As Long, j As Long
Dim z(3, N, N)
Dim tmax As Long
Dim 境界条件 As String
'境界条件 = "固定端"
境界条件 = "自由端"
dt = 0.02
tmax = 25 '25秒後
'波の初期条件の決定
For i = 0 To N
For j = 0 To (N - 1)
If i > (0 * N) And i < (1 * N) And j > (0.4 * N) And j < (0.6 * N) Then
z(0, i, j) = 10 * Cos(3.14159265 * ((j - 50) / 20))
Else
z(0, i, j) = 0
End If
Next j
Next i
'初期状態から次の状態を計算する
For i = 1 To (N - 1 - 1)
For j = 1 To (N - 1 - 1)
z(1, i, j) = z(0, i, j) + ccc ^ 2 / 2 * dt ^ 2 / (dd ^ 2) * (z(0, i + 1, j) + z(0, i - 1, j) + z(0, i, j + 1) + z(0, i, j - 1) - 4 * z(0, i, j))
Next j
Next i
'以降、波の状態を計算する
t = 2 * dt
Do
For i = 1 To (N - 1 - 1)
For j = 1 To (N - 1 - 1)
z(2, i, j) = 2 * z(1, i, j) - z(0, i, j) + ccc ^ 2 * dt ^ 2 / (dd ^ 2) * (z(1, i + 1, j) + z(1, i - 1, j) + z(1, i, j + 1) + z(1, i, j - 1) - 4 * z(1, i, j))
Next j
Next i
'境界条件
If 境界条件 = "固定端" Then ' 全周-固定端
For i = 0 To (N - 1)
z(2, i, 0) = 0
z(2, i, N - 1) = 0
z(2, 0, i) = 0
z(2, N - 1, i) = 0
Next i
Else ' 全周-自由端
For i = 0 To (N - 1)
z(2, i, 0) = z(2, i, 1)
z(2, i, N - 1) = z(2, i, N - 1 - 1)
z(2, 0, i) = z(2, 1, i)
z(2, N - 1, i) = z(2, N - 1 - 1, i)
Next i
End If
'次の計算のために配列の数値を入れかえ 1→0 2→1
For i = 0 To (N - 1)
For j = 0 To (N - 1)
z(0, i, j) = z(1, i, j)
z(1, i, j) = z(2, i, j)
Next j
Next i
t = t + dt
Loop While t <= (tmax - dt)
'最後の結果を出力
For i = 0 To (N - 1)
For j = 0 To (N - 1)
Cells(i + 5, j + 5) = z(2, i, j)
Next j
Next i
End SubN=100メッシュの場合 : さざなみが立つ。 メッシュが粗く高調波成分が再現できない?

dtが粗いと計算は破綻する (dt=2 tmax=10の例)
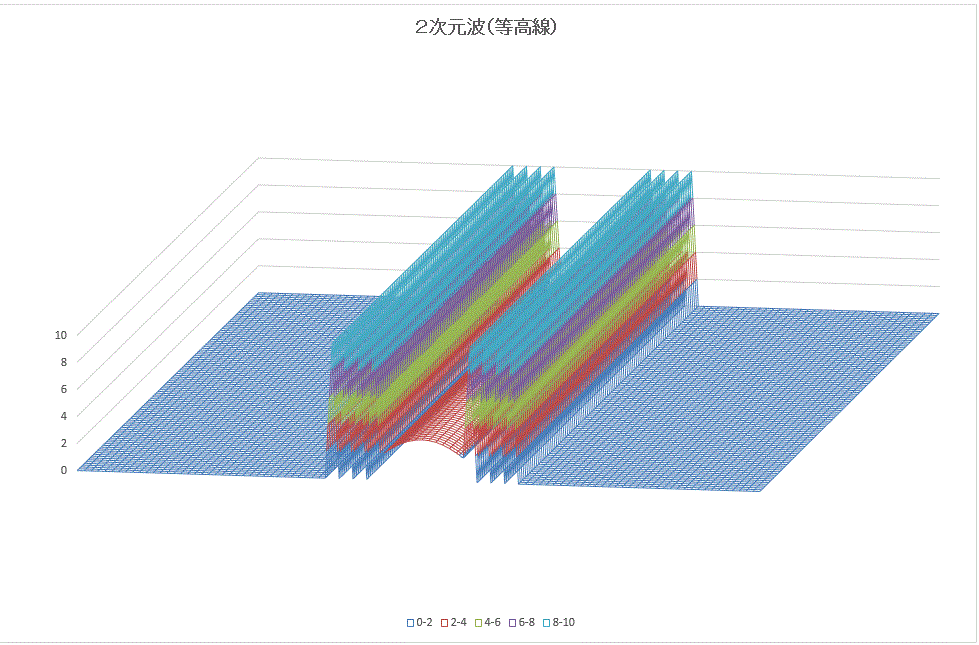
N=500メッシュの場合 ・・・ 計算時間はN=100の125倍
