娘核種1つ 娘核種2つ 核種3つ以上 Cs-137 ルンゲ=クッタで解く
娘核種が 79%:21%の比率で2つできる場合 ※下記は、 λ2=λ3=0 つまり、娘核種が安定核種の例
dN3/dt = 0.21*λ1・N1 - λ3・N3 — 娘2核種
dN2/dt = 0.79*λ1・N1 - λ2・N2 — 娘1核種
dN1/dt = - λ1・N1
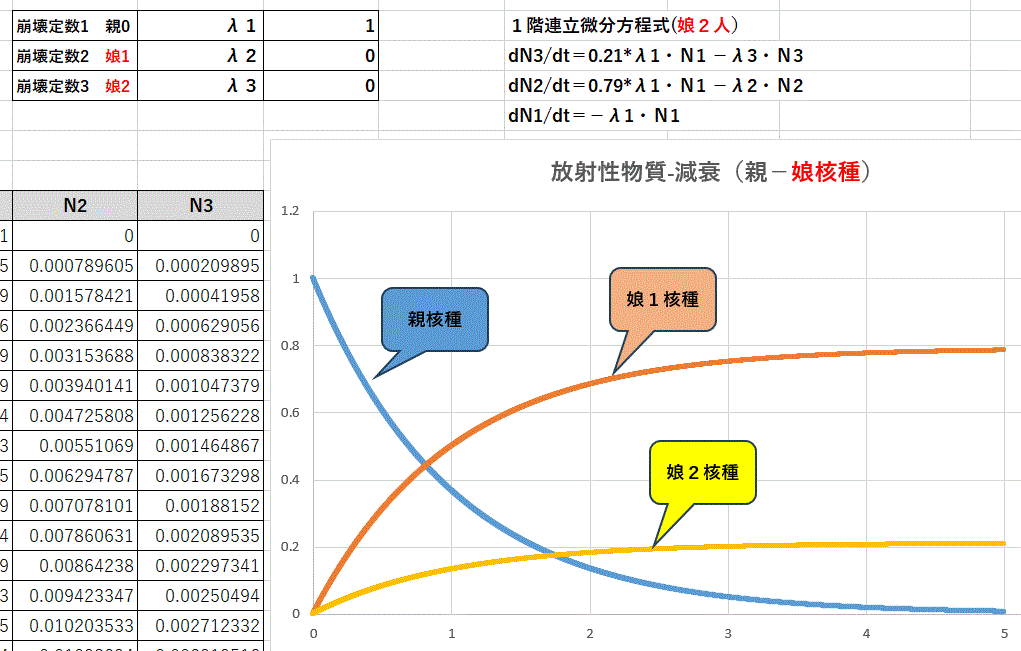
(画像を押すと拡大)
Option Explicit
Sub 放射能_娘2()
Dim t As Double, dt As Double '時間 Exel VBA
Dim N(20) As Double 'mol数 20核種
Dim λ(20) As Double '崩壊定数
Dim ans As Variant
Dim cnt1 As Long
Dim sh As Worksheet
Dim 終了時刻 As Double
Set sh = ThisWorkbook.Worksheets(1)
dt = 0.001
'初期条件----------------------------------
N(1) = 1 '1mol 親
N(2) = 0 '0mol 娘
N(3) = 0 '0mol 娘2
λ(1) = 1 '崩壊定数 親
λ(2) = 0 '崩壊定数 娘
λ(3) = 0 '崩壊定数 娘2
cnt1 = 0
終了時刻 = 5
'------------------------------------------
With sh '表記
.Cells(9, 4).Value = "t" 't
.Cells(9, 5).Value = "N1" 'N1 mol
.Cells(9, 6).Value = "N2" 'N2 mol
.Cells(9, 7).Value = "N3" 'N3 mol
End With
sh.Range("D10:G500000").ClearContents
Do While t <= 終了時刻
With sh
.Cells(cnt1 + 10, 4).Value = t 't
.Cells(cnt1 + 10, 5).Value = N(1) 'N1 mol
.Cells(cnt1 + 10, 6).Value = N(2) 'N2 mol
.Cells(cnt1 + 10, 7).Value = N(3) 'N3 mol
End With
cnt1 = cnt1 + 1
ans = RK4(t, dt, λ, N) ' ルンゲ=クッタ
N(3) = ans(3)
N(2) = ans(2)
N(1) = ans(1)
t = t + dt
Loop
sh.Range("N3") = Time
End Sub
Function RK4(ByVal t, ByVal dt, ByVal λ, ByVal N) As Variant
'下準備-----------------------------------------------------
Dim LL(20) 'λ
Dim NN1(20), NN2(20), NN3(20), NN4(20) 'N
Dim k1NN(20), k2NN(20), k3NN(20), k4NN(20) 'k1NN--k4NN(識別番号)
LL(1) = λ(1)
LL(2) = λ(2)
LL(3) = λ(3)
'下準備-----------------------------------------------------
'k1
NN1(3) = N(3) '前処理
NN1(2) = N(2) '前処理
NN1(1) = N(1) '前処理
k1NN(3) = dt * 娘2関数(t, LL, NN1)
k1NN(2) = dt * 娘関数(t, LL, NN1)
k1NN(1) = dt * 親関数(t, LL, NN1)
'k2
NN2(3) = NN1(3) + k1NN(3) / 2 '前処理
NN2(2) = NN1(2) + k1NN(2) / 2 '前処理
NN2(1) = NN1(1) + k1NN(1) / 2 '前処理
k2NN(3) = dt * 娘2関数(t + dt / 2, LL, NN2)
k2NN(2) = dt * 娘関数(t + dt / 2, LL, NN2)
k2NN(1) = dt * 親関数(t + dt / 2, LL, NN2)
'k3
NN3(3) = NN1(3) + k2NN(3) / 2 '前処理
NN3(2) = NN1(2) + k2NN(2) / 2 '前処理
NN3(1) = NN1(1) + k2NN(1) / 2 '前処理
k3NN(3) = dt * 娘2関数(t + dt / 2, LL, NN3)
k3NN(2) = dt * 娘関数(t + dt / 2, LL, NN3)
k3NN(1) = dt * 親関数(t + dt / 2, LL, NN3)
'k4
NN4(3) = NN1(3) + k3NN(3) '前処理
NN4(2) = NN1(2) + k3NN(2) '前処理
NN4(1) = NN1(1) + k3NN(1) '前処理
k4NN(3) = dt * 娘2関数(t + dt, LL, NN4)
k4NN(2) = dt * 娘関数(t + dt, LL, NN4)
k4NN(1) = dt * 親関数(t + dt, LL, NN4)
NN1(3) = NN1(3) + 1 / 6 * (k1NN(3) + 2 * k2NN(3) + 2 * k3NN(3) + k4NN(3))
NN1(2) = NN1(2) + 1 / 6 * (k1NN(2) + 2 * k2NN(2) + 2 * k3NN(2) + k4NN(2))
NN1(1) = NN1(1) + 1 / 6 * (k1NN(1) + 2 * k2NN(1) + 2 * k3NN(1) + k4NN(1))
RK4 = NN1
End Function
Function 娘2関数(ByVal t, ByVal LL, ByVal NN) As Double
'd/dt・N3(t)=0.21*λ1・N1 -λ3・N3
娘2関数 = 0.21 * LL(1) * NN(1) - LL(3) * NN(3)
End Function
Function 娘関数(ByVal t, ByVal LL, ByVal NN) As Double
'd/dt・N2(t)=0.79*λ1・N1 -λ2・N2
娘関数 = 0.79 * LL(1) * NN(1) - LL(2) * NN(2)
End Function
Function 親関数(ByVal t, ByVal LL, ByVal NN) As Double
'dN1/dt = -λ1・N1
親関数 = -LL(1) * NN(1)
End Function