-証明-
以下、背理法により、πが無理数であることを証明する。
πが、有理数であるとすると、互いに素な整数p,qにより
π=q/pとあらわせることになる。
——————————————————————————
今、関数
f(x)=x^n・(q – p・x)^n/n! (p,q,nは自然数とする)
を考える。
この関数の(q – p・x)^nの部分は、二項定理に
従って、n+1項の多項式に展開をすることができる。
したがって、関数f(x)は、x^n~x^2nのxの多項式になり
n
f(x)=1/n!・ ΣAk・x^(n+k)
k=0
と書きなおすことができる。
ここで、 f(x)の j 回微分を f(j)(x)と書き表すと
■ j<nの場合、※※ ゼロになるパターン
f(j)(0)=0
■ j>2nの場合、
f(j)(0)=0
■ n≦j≦2nの場合、
f(j)(0)=A(j-n)・j!/n!
となる。 このとき f(j)(0)は、整数となる。(∵ 分母のn!は うまく消せるため)
ここで、
F(x)=f(x)-f(2)(x)+f(4)(x)-・・・・・・・・+(-1)^n・f(2n)(x)
という関数を考えると
任意のj に対し f(j)(0)が、整数なので、F(0)も整数になる。 (※単に足し算、引き算しているだけだから)
又、
f(x)=f(q/p-x) なので、以下のことがいえる
f(x)=f(q/p-x)
f(j)(x)=(-1)^j・f(j)(q/p-x)
したがって
f(j)(π)=(-1)^j・f(j)(q/p-π)=(-1)^j・f(j)(0)
故に、
F(π)も、F(0)と同様に整数といえるだろう。
天下り的に、ここで、 F(x) とF(x)の2階微分は、
F(x) =f(x)-f(2)(x)+f(4)(x)-・・・・・・・・+(-1)^n・f(2n)(x)
F(2)(x)= +f(2)(x)-f(4)(x)+・・・・・・・・-(-1)^n・f(2n)(x)+(-1)^(n+2)・f(2n+2)(x)
さらに これらの式を使って
d/dx・( F(1)(x)・sinx-F(x)・cosx)= F(2)(x)・sinx +F(x)・sinx
=f(x)・sinx+(-1)^(n+2)・f(2n+2)(x)・sinx ※※ ゼロになるパターン
=f(x)・sinx
となる。
上式を使って 0~πの間で以下の積分を考えよう。
π π
∫f(x)・sinx dx=〔 F(1)(x)・sinx-F(x)・cosx 〕 =F(π)+F(0)
0 0
この積分値は、整数ということになる。・・・結論①
ところで、xが、0~πの間では、
0<sinx<1
0<q-p・x<q
0<x<π
なので ※※ 及び、f(x)の定義より
0<f(x)・sinx < x^n・(q – p・x)^n/n! < (π・q)^n/n!
したがって、
π π
0 < ∫f(x)・sinx dx < ∫(π・q)^n/n! dx = π^(n+1)・q^n/n!
0 0
が成り立つ。
ところが、n を適当に大きくとっていくと
π^(n+1)・q^n/n! → 0に近づくので
π
0 < ∫f(x)・sinx dx < 1
0
すなわち、
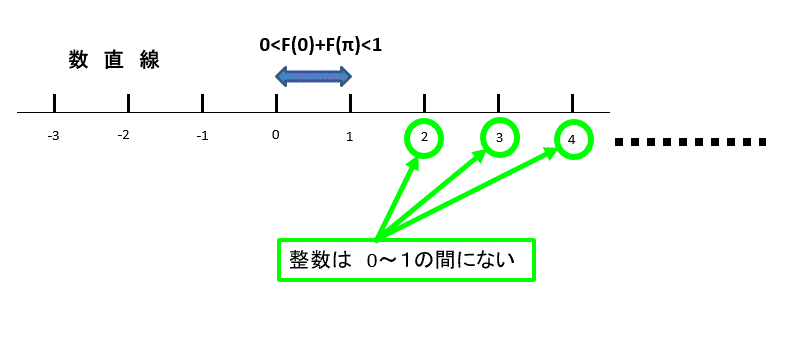
0 < F(π)+F(0) < 1 ・・・結論②
とできる。
この結論②は、前半で導き出した結論①、nに関係なく 『F(π)+F(0)が、整数である』と導けたことに反する。
(※整数は0~1の間にはありません。 数直線を描いて確認する)
したがって、背理法により、πは無理数といえる。 (証明終) ※一部、口語に変更。
———————————————————————————–