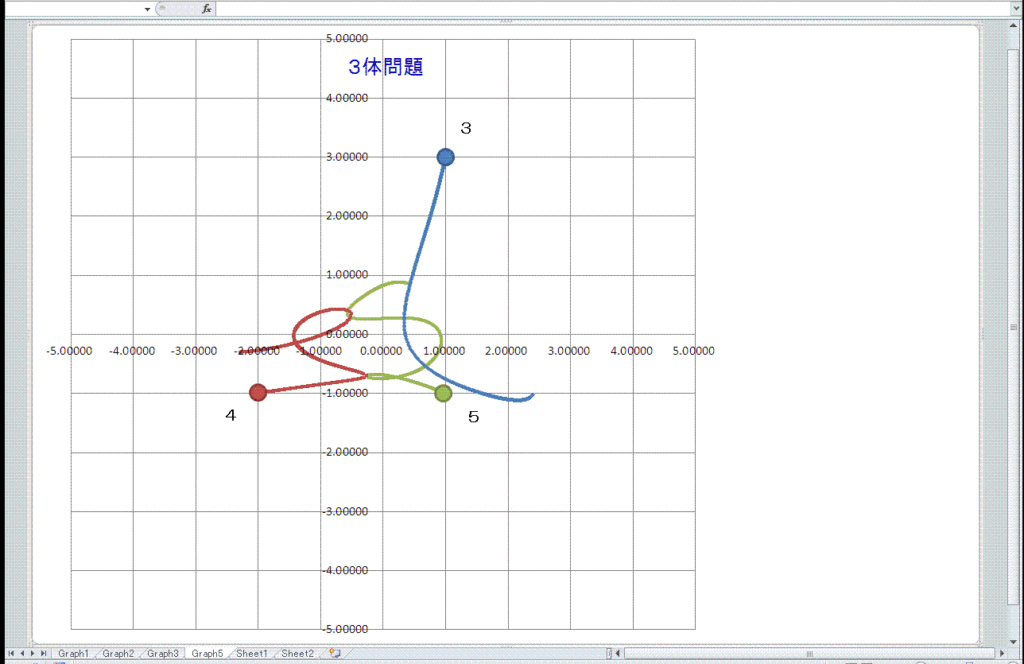
4次のルンゲ=クッタで解く。 (t=0~5秒, dt=0.0001 秒)
条件:G=1 M1=3,M2=4,M3=5 M2-M3間=3, M3-M1間=4, M1-M2間=5
万有引力(逆2乗)法則 a =-G・M/r^2×{(r→)/|r|}
Option Explicit
Option Base 1
Dim m(3) As Double
Public Const G As Double = 1 '万有引力定数
Sub メインルーチン()
Dim t As Double, dt As Double ' 時間
Dim rr(3, 3) As Double ' rr(識別番号,軸成分)
Dim vv(3, 3) As Double ' vv(識別番号,軸成分)
Dim ans As Variant
Dim cnt0 As Long, cnt1 As Long
Dim sh As Worksheet
Dim 終了時刻 As Double
Set sh = ThisWorkbook.Worksheets(1)
sh.Range("C10:AD1048576").ClearContents ' データ消去
sh.Range("N2") = Time ' 開始時刻
'初期条件
m(1) = 3 ' 質量1
m(2) = 4 ' 質量2
m(3) = 5 ' 質量3
rr(1, 1) = 1 '(識別番号,軸成分)
rr(1, 2) = 3 '(識別番号,軸成分)
rr(1, 3) = 0 '(識別番号,軸成分)
rr(2, 1) = -2 '(識別番号,軸成分)
rr(2, 2) = -1 '(識別番号,軸成分)
rr(2, 3) = 0 '(識別番号,軸成分)
rr(3, 1) = 1 '(識別番号,軸成分)
rr(3, 2) = -1 '(識別番号,軸成分)
rr(3, 3) = 0 '(識別番号,軸成分)
vv(1, 1) = 0 '(識別番号,軸成分)
vv(1, 2) = 0 '(識別番号,軸成分)
vv(1, 3) = 0 '(識別番号,軸成分)
vv(2, 1) = 0 '(識別番号,軸成分)
vv(2, 2) = 0 '(識別番号,軸成分)
vv(2, 3) = 0 '(識別番号,軸成分)
vv(3, 1) = 0 '(識別番号,軸成分)
vv(3, 2) = 0 '(識別番号,軸成分)
vv(3, 3) = 0 '(識別番号,軸成分)
終了時刻 = 5
dt = 0.0001
cnt0 = 0
cnt1 = 0
With sh '表記
.Cells(9, 4).Value = "t" 't
.Cells(9, 5).Value = "x1" 'x1
.Cells(9, 6).Value = "y1" 'y1
.Cells(9, 7).Value = "x2" 'x2
.Cells(9, 8).Value = "y2" 'y2
.Cells(9, 9).Value = "x3" 'x3
.Cells(9, 10).Value = "y3" 'y3
End With
Do While t < 終了時刻
With sh
.Cells(cnt1 + 10, 4).Value = t 't
.Cells(cnt1 + 10, 5).Value = rr(1, 1) 'M1 x
.Cells(cnt1 + 10, 6).Value = rr(1, 2) 'M1 y
.Cells(cnt1 + 10, 7).Value = rr(2, 1) 'M2 x
.Cells(cnt1 + 10, 8).Value = rr(2, 2) 'M2 y
.Cells(cnt1 + 10, 9).Value = rr(3, 1) 'M3 x
.Cells(cnt1 + 10, 10).Value = rr(3, 2) 'M3 y
cnt1 = cnt1 + 1
End With
ans = RK4(t, dt, m, rr, vv) ' ルンゲ=クッタ
rr(1, 1) = ans(1)
rr(1, 2) = ans(2)
rr(1, 3) = ans(3)
vv(1, 1) = ans(4)
vv(1, 2) = ans(5)
vv(1, 3) = ans(6)
rr(2, 1) = ans(7)
rr(2, 2) = ans(8)
rr(2, 3) = ans(9)
vv(2, 1) = ans(10)
vv(2, 2) = ans(11)
vv(2, 3) = ans(12)
rr(3, 1) = ans(13)
rr(3, 2) = ans(14)
rr(3, 3) = ans(15)
vv(3, 1) = ans(16)
vv(3, 2) = ans(17)
vv(3, 3) = ans(18)
cnt0 = cnt0 + 1
t = t + dt
Loop
sh.Range("N3") = Time
End Sub
Function RK4(ByVal t, ByVal dt, m, ByVal r0, ByVal v0) As Variant
'下準備----------------------------
Dim ret(18)
Dim r1(3, 3), r2(3, 3), r3(3, 3), r4(3, 3) ' r(識別番号,軸成分)
Dim v1(3, 3), v2(3, 3), v3(3, 3), v4(3, 3) ' v(識別番号,軸成分)
Dim k1rr(3, 3), k2rr(3, 3), k3rr(3, 3), k4rr(3, 3) ' k1rr(識別番号,軸成分)
Dim k1vv(3, 3), k2vv(3, 3), k3vv(3, 3), k4vv(3, 3) ' k1vv(識別番号,軸成分)
Dim 番号 As Integer, 軸 As Integer
'下準備----------------------------
'k1
For 番号 = 1 To 3
For 軸 = 1 To 3
v1(番号, 軸) = v0(番号, 軸) 'v(識別番号,軸成分) (3,3) 3体×3次元 前処理
r1(番号, 軸) = r0(番号, 軸) 'r(識別番号,軸成分) (3,3) 3体×3次元 前処理
Next 軸
Next 番号
For 番号 = 1 To 3 '識別番号
For 軸 = 1 To 3 '軸成分
k1vv(番号, 軸) = dt * 速度変位成分_func(番号, 軸, t, r1, v1) '速度変位総和 m/s^2 ★dv/dt 3体×3次元=9連立
k1rr(番号, 軸) = dt * 位置変位成分_func(番号, 軸, t, r1, v1) '位置変位成分 m/s ★dx/dt 3体×3次元=9連立
Next 軸
Next 番号
'k2
For 番号 = 1 To 3
For 軸 = 1 To 3
v2(番号, 軸) = v1(番号, 軸) + k1vv(番号, 軸) / 2 'v(識別番号,軸成分) (3,3) 前処理
r2(番号, 軸) = r1(番号, 軸) + k1rr(番号, 軸) / 2 'r(識別番号,軸成分) (3,3) 前処理
Next 軸
Next 番号
For 番号 = 1 To 3 '識別番号
For 軸 = 1 To 3 '軸成分
k2vv(番号, 軸) = dt * 速度変位成分_func(番号, 軸, t + dt / 2, r2, v2) '速度変位総和 m/s^2 ★dv/dt 3体×3次元=9連立
k2rr(番号, 軸) = dt * 位置変位成分_func(番号, 軸, t + dt / 2, r2, v2) '位置変位成分 m/s ★dx/dt 3体×3次元=9連立
Next 軸
Next 番号
'k3
For 番号 = 1 To 3
For 軸 = 1 To 3
v3(番号, 軸) = v1(番号, 軸) + k2vv(番号, 軸) / 2 'v(識別番号,軸成分) (3,3) 前処理
r3(番号, 軸) = r1(番号, 軸) + k2rr(番号, 軸) / 2 'r(識別番号,軸成分) (3,3) 前処理
Next 軸
Next 番号
For 番号 = 1 To 3 '識別番号
For 軸 = 1 To 3 '軸成分
k3vv(番号, 軸) = dt * 速度変位成分_func(番号, 軸, t + dt / 2, r3, v3) '速度変位総和 m/s^2 ★dv/dt 3体×3次元=9連立
k3rr(番号, 軸) = dt * 位置変位成分_func(番号, 軸, t + dt / 2, r3, v3) '位置変位成分 m/s ★dx/dt 3体×3次元=9連立
Next 軸
Next 番号
'k4
For 番号 = 1 To 3
For 軸 = 1 To 3
v4(番号, 軸) = v1(番号, 軸) + k3vv(番号, 軸) 'v(識別番号,軸成分) (3,3) 前処理
r4(番号, 軸) = r1(番号, 軸) + k3rr(番号, 軸) 'r(識別番号,軸成分) (3,3) 前処理
Next 軸
Next 番号
For 番号 = 1 To 3 '識別番号
For 軸 = 1 To 3 '軸成分
k4vv(番号, 軸) = dt * 速度変位成分_func(番号, 軸, t + dt, r4, v4) '速度変位総和 m/s^2 ★dv/dt 3体×3次元=9連立
k4rr(番号, 軸) = dt * 位置変位成分_func(番号, 軸, t + dt, r4, v4) '位置変位成分 m/s ★dx/dt 3体×3次元=9連立
Next 軸
Next 番号
For 番号 = 1 To 3
For 軸 = 1 To 3
v1(番号, 軸) = v1(番号, 軸) + 1 / 6 * (k1vv(番号, 軸) + 2 * k2vv(番号, 軸) + 2 * k3vv(番号, 軸) + k4vv(番号, 軸)) ' m/s
r1(番号, 軸) = r1(番号, 軸) + 1 / 6 * (k1rr(番号, 軸) + 2 * k2rr(番号, 軸) + 2 * k3rr(番号, 軸) + k4rr(番号, 軸)) ' m
Next 軸
Next 番号
'便宜的に戻り値を行列 ret(18)でまとめ
ret(1) = r1(1, 1)
ret(2) = r1(1, 2)
ret(3) = r1(1, 3)
ret(4) = v1(1, 1)
ret(5) = v1(1, 2)
ret(6) = v1(1, 3)
ret(7) = r1(2, 1)
ret(8) = r1(2, 2)
ret(9) = r1(2, 3)
ret(10) = v1(2, 1)
ret(11) = v1(2, 2)
ret(12) = v1(2, 3)
ret(13) = r1(3, 1)
ret(14) = r1(3, 2)
ret(15) = r1(3, 3)
ret(16) = v1(3, 1)
ret(17) = v1(3, 2)
ret(18) = v1(3, 3)
RK4 = ret
End Function
Function 速度変位成分_func(ByVal 被番号, ByVal 軸, ByVal t, ByVal r, ByVal v) As Double ' (速度変位 m/s^2)を返す
Dim sum_a As Double
Dim rrr As Double
Dim 差異(3) As Double
Dim 基準天体 As Integer
rrr = 0 ' 初期化
sum_a = 0 ' 初期化
' dv/dt = -G・M・(→r)/r^3 ・・・ 万有引力の法則
For 基準天体 = 1 To 3 '番号
If 被番号 <> 基準天体 Then ' 相違する場合だけ計算する
差異(1) = r(被番号, 1) - r(基準天体, 1) 'r(識別番号,軸成分) x成分
差異(2) = r(被番号, 2) - r(基準天体, 2) 'r(識別番号,軸成分) y成分
差異(3) = r(被番号, 3) - r(基準天体, 3) 'r(識別番号,軸成分) z成分
rrr = (差異(1) ^ 2 + 差異(2) ^ 2 + 差異(3) ^ 2) ^ 0.5 'r = √(x^2+y^2+z^2)
sum_a = -G * m(基準天体) * 差異(軸) / rrr / rrr / rrr + sum_a '相違し、且つ、計算する軸成分だけを積算する
End If
Next 基準天体
速度変位成分_func = sum_a '加速度 1成分のみ
End Function
Function 位置変位成分_func(ByVal 被番号, ByVal 軸, ByVal t, ByVal r, ByVal v) As Double ' (位置変位 m/s)を返す
' dx/dt = v
位置変位成分_func = v(被番号, 軸) '単に速度ベクトルを返す 1成分のみ
End Function
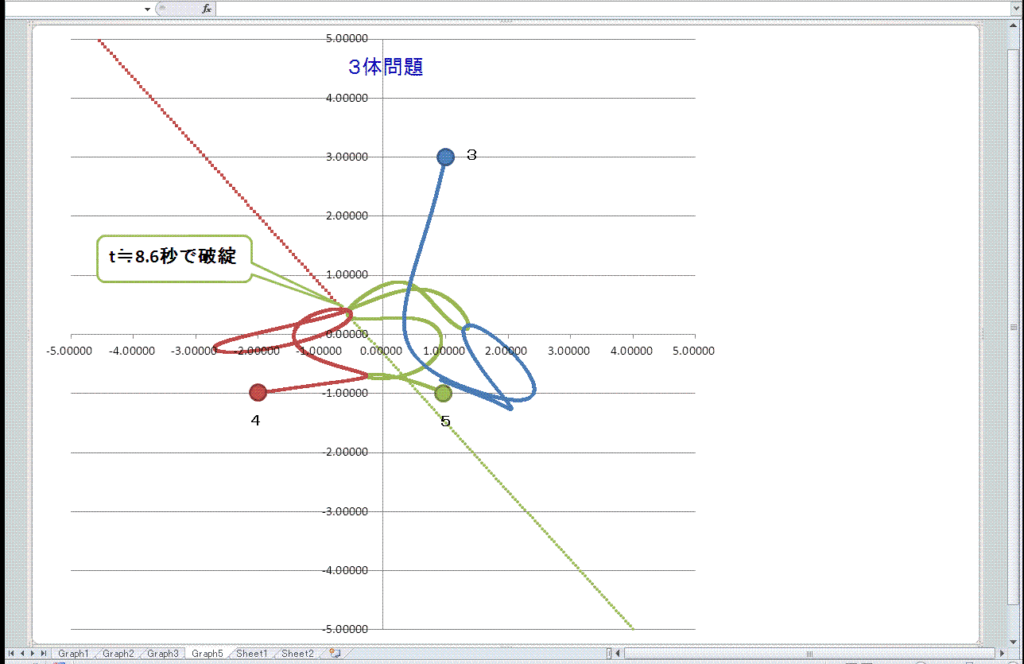
(dt=0.0001にて 約8.6秒後に計算が破綻する様子)
《自動幅制御:誤差見積もり》
結局、通常のdtでの計算結果と dt/2で2回計算の結果とを比較評価しながら
許容される場合はそのまま、超える場合は dt を半分にするアルゴリズムを
上位に配置し(つまり、自動幅制御をしながら)計算させた。
大変カオティックな問題なので、最終的に区間許容誤差=10^-11 としてはじめて
Szebehely, V. & Peters, C. F. (16 May 1967) Complete Solution
とほぼ同じ図形を得た。 (但し、有効数字は1~2桁まで低下 ;t=60)
ルンゲ=クッタ 4次 自動幅制御での結果 (t= 0~70)
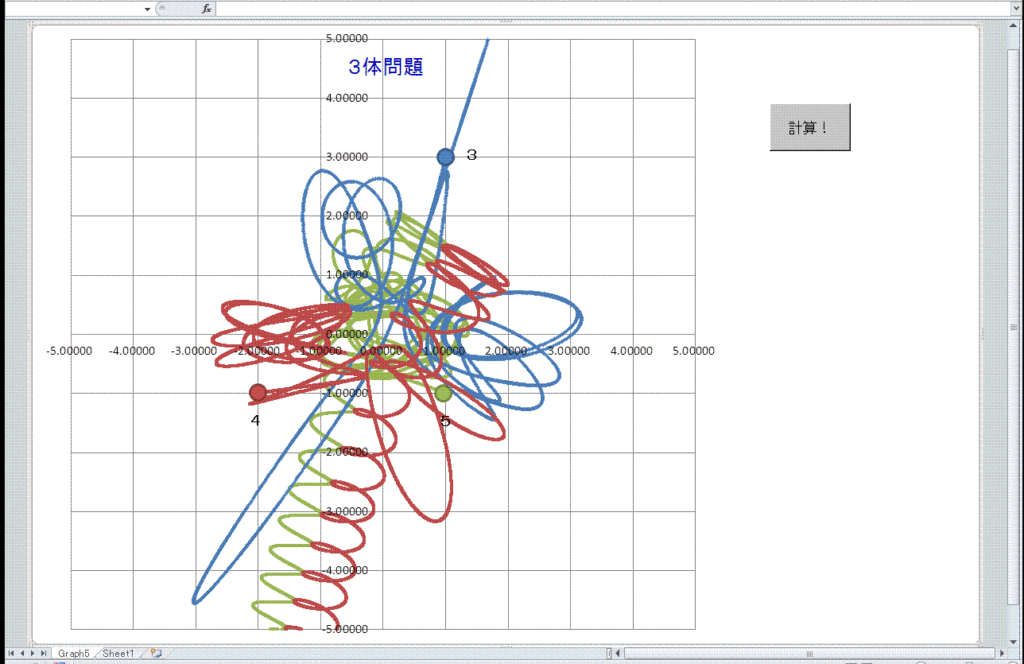
区間許容誤差=10^-13にて計算すると 有効数字は3桁強まで改善 ;t=60
区間許容誤差=10^-16にて計算すると 有効数字 は5桁 まで改善 ;t=60
区間許容誤差=10^-19にて計算すると 有効数字 は6桁 まで改善 ;t=60
(条件:十進BASIC 1000桁モード)
34桁版/3体問題 ・・・ もう4倍精度(約34桁)くらいが 標準で も良い時代だと思う。
————————————————————————————————
参考:パソコンで見る天体の動き p175-183 地人書館
EXELで繰る! ここまでできる科学技術計算 p59-p61 丸善出版
Cによる数値計算 p183-184 朝倉書店 TST