YouTubeのヨビノリさんがおもしろい話をしていた。 期待値がマイナスの2つのゲーム(A,B)を
コイントス(コインの裏表)で決めると期待値がプラスのゲーム(C)に変わる場合があるらしい 逆パロンドはこちら
ゲームA : 52%負け1ドル減 48%勝ち1ドル増 ※ゲームA 期待値マイナス
ゲームB : (所持金により変わる)
所持金が3で割れる場合 1%勝ち1ドル増 99%負け1ドル減
所持金が3で割れない場合 85%勝ち1ドル増 15%負け1ドル減 ※ゲームB 期待値マイナス(わかりにくいけど)
ゲームC : ゲームA/ゲームBをコインの裏表で決める ※ゲームC 期待値プラス
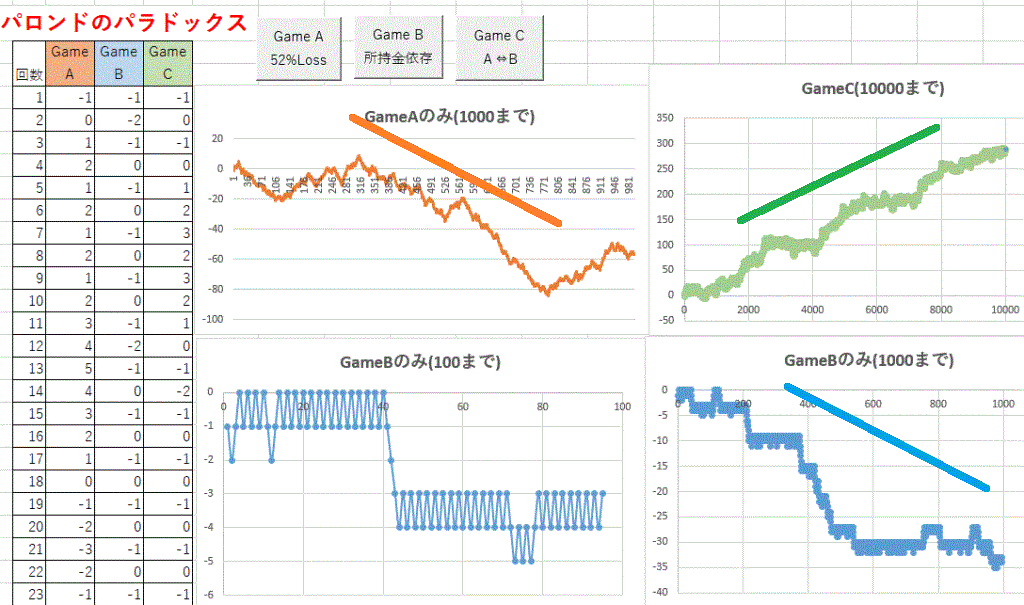
画像を押すと拡大
'パロンドのパラドックス
Option Explicit
'★★★
Sub GameC()
Dim 所持金 As Long, KK As Long
Dim ws As Worksheet
Set ws = ThisWorkbook.Worksheets(1)
所持金 = 0
For KK = 1 To 10000
If Rnd() < 0.5 Then
所持金 = 所持金 + GameA増減 'GameA
Else
所持金 = 所持金 + GameB増減(所持金) 'GameB
End If
ws.Cells(KK + 5, 9) = 所持金 '印刷
Next KK
End Sub
'★★★
Sub GameB()
Dim 所持金 As Long, KK As Long
Dim ws As Worksheet
Set ws = ThisWorkbook.Worksheets(1)
所持金 = 0
For KK = 6 To 10000
所持金 = 所持金 + GameB増減(所持金)
ws.Cells(KK, 8) = 所持金
Next KK
End Sub
'★★★
Sub GameA()
Dim 所持金 As Long, KK As Long
Dim ws As Worksheet
Set ws = ThisWorkbook.Worksheets(1)
所持金 = 0
For KK = 6 To 10000
所持金 = 所持金 + GameA増減()
ws.Cells(KK, 7) = 所持金
Next KK
End Sub
'◆◆◆
Function GameB増減(所持金)
Dim 増減 As Long
If (所持金 Mod 3) = 0 Then
If Rnd() < 0.01 Then
増減 = 1 '1%増
Else
増減 = -1 '99%減
End If
ElseIf (所持金 Mod 3) <> 0 Then
If Rnd() < 0.85 Then
増減 = 1 '85%増
Else
増減 = -1 '15%減
End If
End If
GameB増減 = 増減
End Function
'◆◆◆
Function GameA増減()
Dim 増減 As Long
If Rnd() < 0.52 Then
増減 = -1 '52%減
Else
増減 = 1 '48%増
End If
GameA増減 = 増減
End Function
こういったことに気づくのは一般に数学者だと思っていました。 でも、パロンド先生は物理学者で
意外だったのは、1964年生まれのごく最近のスペイン人。 有名科学者と言えば 19世紀のフランス、
ドイツが頭に浮かぶところですが 今回の発見者が ごく最近のスペイン人という事実は パロンドの
パラドックス 同様、自分には 『直感に反する事実』 でありました。