３体問題

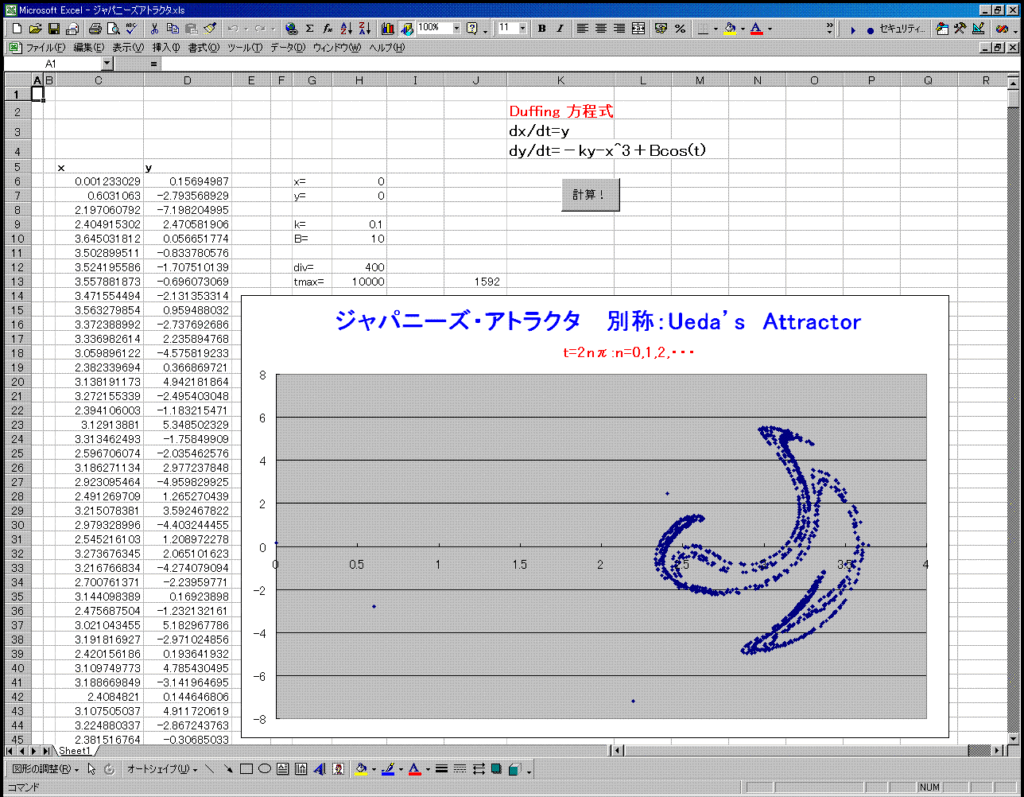
ジャパニーズ・アトラクタ（Ueda’s Attractor）を描く 　
　
※Duffing方程式で　同位相 t=2nπ；n=0,1,2・・・をプロットしていく。

dx/dt = y
dy/dt = -ky-x^3+Bcos(t)

(例）k=0.1　B=10 　t=2nπ；n=0,1,2・・・ (初期値：x=0　y=0)の場合

Sub Jp_ATR()
Dim k0(2), k1(2), k2(2), k3(2)

div = 400
tmax = 10000

dt = 2 * 3.14159265 / div
t = 0
x = 0
y = 0


cnt = 0
cnt2 = 0
   
    Do

        k0(0) = dt * f1(t, x, y)
        k0(1) = dt * f2(t, x, y)
       
        k1(0) = dt * f1(t + dt / 2, x + k0(0) / 2, y + k0(1) / 2)
        k1(1) = dt * f2(t + dt / 2, x + k0(0) / 2, y + k0(1) / 2)
       
        k2(0) = dt * f1(t + dt / 2, x + k1(0) / 2, y + k1(1) / 2)
        k2(1) = dt * f2(t + dt / 2, x + k1(0) / 2, y + k1(1) / 2)
       
        k3(0) = dt * f1(t + dt, x + k2(0), y + k2(1))
        k3(1) = dt * f2(t + dt, x + k2(0), y + k2(1))
       
        x = x + (k0(0) + 2 * k1(0) + 2 * k2(0) + k3(0)) / 6
        y = y + (k0(1) + 2 * k1(1) + 2 * k2(1) + k3(1)) / 6
   
      If cnt Mod div = 0 Then
        Worksheets(1).Cells(6 + cnt2, 3) = x
        Worksheets(1).Cells(6 + cnt2, 4) = y
        cnt2 = cnt2 + 1
      End If
     
    cnt = cnt + 1
    t = t + dt

    Loop While t < tmax


End Sub

Function f1(t, x, y)
f1 = y
End Function

Function f2(t, x, y)
k = 0.1
b = 10
f2 = -k * y - x ^ 3 + b * Cos(t)
End Function