3次元へ適用 (2階微分方程式:3次元)
《物理の実験》 ・・・ 例)残推薬と進入速度の関係
あかつきは2010年の金星投入失敗後、2015年以降で再度投入しようとしている。 JAXAのHPを見ると 2011年11月21日
の時点で残推薬が約50kg(ΔV≒250m/s相当)残っていると思われた。
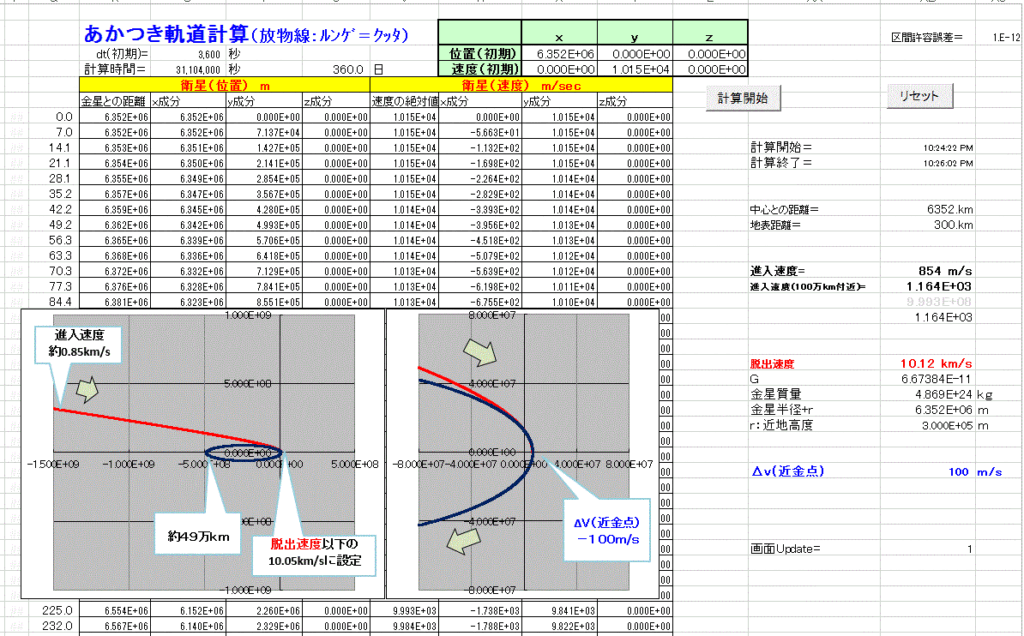
60%マージンをみて近金点にて ΔV=100m/sを施し、近金点速度を10.05km/s(=脱出速度以下)まで減速するとして進入
速度を逆算してみる。
進入速度 = 約0.85km/s (金星に対する)
残推薬の面だけみると、この進入速度以下で金星に近づくことが できれば今の推薬で 比較的余裕をもって軌道投入可能
なのがわかる。
※実際はスイングバイなしで2015年12月投入(予定)となった。
近金点高度 300kmで計算
※※上記は誤差の大きい 金星質量M:4.869×10^24 kg (有効数字4桁) と G:6.67384(80)×10^-11 にて計算している。
尚、 運動エネルギー + 位置エネルギー= 一定 として 50万km付近 と 100万km付近での相対速度を逆算すると以下のとうり。
近金点10.05kmと仮定した場合 ・・ 遠金点49.9万km/16.2日周期投入
| 必要とされる 減速ΔV〔m/s〕 | 減速前の近金点速度〔m/s〕 | 運動エネ+位置エネ kgあたり 〔J〕 | 50万km付近 相対速度 | 100万km付近 相対速度 |
| 280 m/s | 1.0330E+04m/s | 2.2102E+06 | 2.39 km/sec | 2.25 km/sec |
| 260 m/s | 1.0310E+04m/s | 2.0038E+06 | 2.30 km/sec | 2.16 km/sec |
| 240 m/s | 1.0290E+04m/s | 1.7978E+06 | 2.21 km/sec | 2.06 km/sec |
| 220 m/s | 1.0270E+04m/s | 1.5922E+06 | 2.12 km/sec | 1.96 km/sec |
| 200 m/s | 1.0250E+04m/s | 1.3870E+06 | 2.02 km/sec | 1.85 km/sec |
| 180 m/s | 1.0230E+04m/s | 1.1822E+06 | 1.91 km/sec | 1.74 km/sec |
| 160 m/s | 1.0210E+04m/s | 9.7778E+05 | 1.80 km/sec | 1.61 km/sec |
| 140 m/s | 1.0190E+04m/s | 7.7378E+05 | 1.69 km/sec | 1.48 km/sec |
| 120 m/s | 1.0170E+04m/s | 5.7018E+05 | 1.56 km/sec | 1.34 km/sec |
| 100 m/s | 1.0150E+04m/s | 3.6698E+05 | 1.43 km/sec | 1.18 km/sec |
| 80 m/s | 1.0130E+04m/s | 1.6418E+05 | 1.28 km/sec | 0.99 km/sec |
| 60 m/s | 1.0110E+04m/s | -3.8216E+04(楕円) | 1.11 km/sec | 0.76 km/sec |
| 40 m/s | 1.0090E+04m/s | -2.4022E+05(楕円) | 0.90 km/sec | 0.41 km/sec |
| 20 m/s | 1.0070E+04m/s | -4.4182E+05(楕円) | 0.64 km/sec | N/A |
| 0 m/s | 1.0050E+04m/s | -6.4302E+05(楕円) | 0.12 km/sec ※注 | N/A |
※※ G×M=324858.15±0.17 km^3・sec^-2 (有効数字6桁) を利用して計算している。
※ N/A: √(負の数)
※ 1/2・v1^2 -G×M/R1 =1/2・v2^2 -G×M/R2 (従って)⇒ v1=√(2×(1/2・v2^2 -G×M/R2 +G×M/R1))
※注 計算はできるが軌道は存在しない。 (角運動量保存則破綻)
近金点を300kmと仮定した場合の周期・軌道長径・遠点距離・遠点速度の関係も調べてみると以下のとうり。
※2 作用圏の外、 金星の作用圏は62万km <参考> 2012年理科年表(丸善) p79
| 近点速度 v1 | 遠点速度 v2 | 遠点距離 R2 | 軌道長径 2a | 周 期 T |
| 10.12 km/s | N/A | 無限大 |
無限大 |
N/A |
| 10.11km/s | 0.01 km/s | 849.4 万km ※2 |
850.1 万km | 1118.0 日 |
| 10.10 km/s | 0.03 km/s | 232.6 万km ※2 | 233.3 万km | 160.7 日 |
| 10.09 km/s | 0.05 km/s | 134.6 万km ※2 | 135.2 万km | 70.9 日 |
| 10.08 km/s | 0.07 km/s | 94.6 万km ※2 | 95.2 万km | 41.9 日 |
| 10.07 km/s | 0.09 km/s | 72.9 万km ※2 | 73.5 万km | 28.4 日 |
| 10.06 km/s | 0.11 km/s | 59.3 万km | 59.9 万km | 20.9 日 |
| 10.05 km/s | 0.13 km/s | 49.9 万km | 50.5 万km | 16.2 日 |
| 10.04 km/s | 0.15 km/s | 43.1 万km | 43.7 万km | 13.0 日 |
| 10.03 km/s | 0.17 km/s | 37.9 万km | 38.5 万km | 10.8 日 |
| 10.02 km/s | 0.19 km/s | 33.8 万km | 34.4 万km | 9.1 日 |
| 10.01 km/s | 0.21 km/s | 30.5 万km | 31.1 万km | 7.8 日 |
| 10.00 km/s | 0.23 km/s | 27.8 万km | 28.4 万km | 6.8 日 |
| 9.99 km/s | 0.25 km/s | 25.5 万km | 26.1 万km | 6.0 日 |
| 9.98 km/s | 0.27 km/s | 23.5 万km | 24.2 万km | 5.4 日 |
| 9.97 km/s | 0.29 km/s | 21.9 万km | 22.5 万km | 4.8 日 |
| 9.96 km/s | 0.31 km/s | 20.4 万km | 21.0 万km | 4.4 日 |
| 9.95 km/s | 0.33 km/s | 19.1 万km | 19.8 万km | 4.0 日 |
| 9.94 km/s | 0.35 km/s | 18.0 万km | 18.6 万km | 3.6 日 |
| 9.93 km/s | 0.37 km/s | 17.0 万km | 17.6 万km | 3.3 日 |
| 9.92 km/s | 0.39 km/s | 16.1 万km | 16.7 万km | 3.1 日 |
| 9.91 km/s | 0.41 km/s | 15.3 万km | 15.9 万km | 2.9 日 |
| 9.90 km/s | 0.43 km/s | 14.6 万km | 15.2 万km | 2.7 日 |
| 9.89 km/s | 0.45 km/s | 13.9 万km | 14.5 万km | 2.5 日 |
| 9.88 km/s | 0.47 km/s | 13.3 万km | 13.9 万km | 2.3 日 |
| 9.87 km/s | 0.49 km/s | 12.7 万km | 13.3 万km | 2.2 日 |
| 9.86 km/s | 0.51 km/s | 12.2 万km | 12.8 万km | 2.1 日 |
| 9.85 km/s | 0.53 km/s | 11.7 万km | 12.3 万km | 2.0 日 |
- 使用した式 -
周 期 T = 2・π・√(GM^2/(2・E)^3) ・・ 但し、 E = 1/2・v1^2 -G×M/R1 |絶対値|
軌道長径 2a = GM/|E| ・・ 但し、 E = 1/2・v1^2 -G×M/R1 |絶対値|
遠点距離 R2=2a-6051.8km-300km ・・ 金星中心からの距離としている
遠点速度 v2=√(2×(1/2・v1^2 -GM/R1 +GM/R2))
※ G×M=324858.15±0.17 km^3・sec^-2 (有効数字6桁) を利用 : 金星